R-CNN

Posted on

paper：

Rich feature hierarchies for accurate object detection and semantic segmentation -arXiv:1311 CVPR2014

参考文章：

https://blog.csdn.net/wopawn/article/details/52133338

http://www.cnblogs.com/makefile/p/nms.html

Introduction

12年、13年，Alexnet 和 VGGnet 相继诞生， 在分类任务中将传统方法重重地踩在了脚下，深度卷积神经网络开始在计算机视觉领域大放异彩。比分类任务更进一步的检测任务，当然不会被研究者们放过，于是RGB大神（Ross Girshick）的R-CNN横空出世。

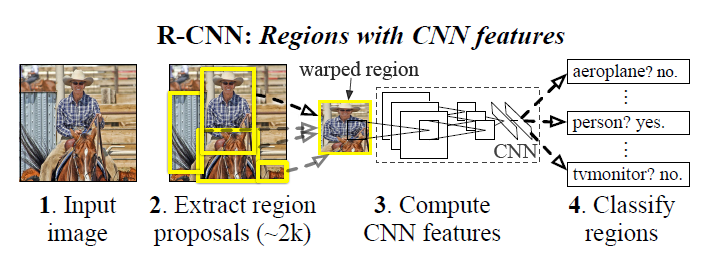
1539947950822

R-CNN 全称为Regions with CNN features，也就是说，它将图像中的某些候选区域（regions）放到CNN中，然后对得到的特征（features）进行检测。从上图可以看出，它的总体流程如下：

  1. 从输入图像提取约个2000候选区域
  2. 对于每个区域，都让其通过一个CNN，得到定长的特征向量
  3. 对于每个feature， 用SVM进行分类

R-CNN是将Deep Learning引入目标检测的开山之作，虽然此时的它还略显臃肿（进行了太多次的CNN运算）。此外，这篇论文还提出了一个重要的思想，即一个任务的预训练模型（如ImageNet）对于另一个任务的训练有很大的帮助，能够缩短其训练时间，也能让其Loss Function更有效地收敛。

也正是由于R-CNN是开山之作，它只是将CNN用于特征提取，其他很多操作仍然采用传统方法，这些方法在后续成熟版本中已经弃用，对于这些细节，如果实在是搞不懂，可以跳过。Faster R-CNN才是重中之重。

Implementation

1.模型设计

首先，使用传统的selective selective方法，从输入图像提取约个2000候选区域（Region Proposal），但是后面的工作（如Faster RCNN）中都用CNN来提取候选区域了，所以SS在这就不做介绍了。想了解的可以看这篇文章https://blog.csdn.net/mao_kun/article/details/50576003

之后，对于每个候选区域，都让其经过Alexnet的卷积层，从而提取出4096维的特征向量。由于Alexnet要求输入的图像大小为227x227，因此对于各种不同大小和纵横比的区域，在通过Alexnet之前需要进行卷曲操作（wrap），从而得到定长的输入Alexnet的图像。

对于每个候选区域，将其4096维的特征向量做每个类别的SVM分类（若类别数目为N，则有N个SVM分类器，每个SVM做二分类，即属于或不属于该类别），得到相对于每个类别的分数。即2000x4096维的特征矩阵与4096xN维的SVM参数矩阵相乘，得到2000xN维的分数矩阵。

对于同一类的2000个候选区域的分数，使用非极大值抑制（non-maximun suppresion，NMS）剔除掉一些重复的相近的候选框，保留一些得分最高的候选框，即保证对于每个物体，只有一个得分最高的框将其选中。关于NMS，详见附录B。

最后，对于N个类别中剩余的候选框，使用N个回归器做回归（称为Bounding-box regression），使得候选框的定位更加准确，得到最终的结果。

2.训练过程

2.1 预训练（pre-training）

在ILSVRC数据集上对AlexNet进行分类训练，得到预训练模型，该模型保存了训练完毕后的AlexNet的参数。

2.2 微调（fine-tuning）

将分类任务上的AlexNet迁移到检测任务上，需要对训练好的AlexNet进行微调，此时输入为候选区域变形后的227x227大小的图像，输出需要将原来的1000维（1000类）改为N+1维（N个类别+背景）。

选定候选区域与标准框（ground truth）的IoU（见附录A）大于等0.5的为正样本，小于0.5的为负样本。即使是这样分，负样本仍比正样本多得多。因此，在每一次的SGD迭代中，选择32个正样本和96个负样本（3:1）为一个mini-batch。

学习率（learning rate）设为0.001，是预训练时的1/10，从而保证在学习新东西时不至于忘记之前的记忆 。

2.3 分类训练

对于每个类别的SVM分类器，选择ground-truth 框作为正样本， 选择与ground-truth的IOU小于0.3的候选框为负样本。同样的，负样本的数目远多于正样本的数目，需要采用负样本挖掘算法（hard negetive mining）选取一部分负样本进行训练。详见附录C。

2.4 回归训练（bounding box regression）

详见附录D。

附录

A.IoU


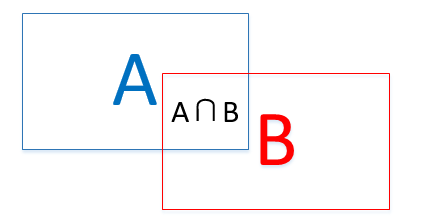
即A与B的交集（intersection）与A与B的并集（union）之比：(A∩B)/(A∪B)

B. 非极大值抑制（Non-maximun suppresion，NMS）

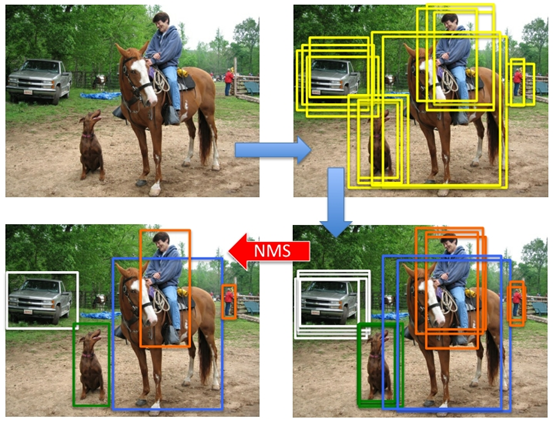
在得到每一类的2000个候选区域后，会遇到上图所示情况，同一个目标会被多个建议框包围，这时需要非极大值抑制操作去除得分较低的候选框以减少重叠框。

其基本操作流程如下：

  1. 对于每一类，按scores大小排序

  2. 找到scores最大的候选框，将其保留，然后分别与其他候选框计算IoU，若IoU大于设定的阈值，则剔除得分较小的那个候选框

  3. 所有候选框遍历完毕后，选择socres第二大的候选框，将其保留，重复步骤2。

  4. 重复步骤3，直到所有的候选框都被筛选过。

注：对于得分低于某一阈值的候选框，应该直接剔除， 但是文章没有说明何时剔除。

Python代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import numpy as np

def py_cpu_nms(dets, thresh):
    """Pure Python NMS baseline."""
    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]
    scores = dets[:, 4]
    
    #每一个检测框的面积
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)
    #按照score置信度降序排序
    order = scores.argsort()[::-1]

    keep = []  #保留的结果框集合
    while order.size > 0:
        i = order[0]
        keep.append(i)  #保留该类剩余box中得分最高的一个
        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])

        #计算相交的面积,不重叠时面积为0
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        #计算IoU：重叠面积 /（面积1+面积2-重叠面积）
        ovr = inter / (areas[i] + areas[order[1:]] - inter)
		#保留IoU小于阈值的box
        inds = np.where(ovr <= thresh)[0]
        order = order[inds + 1] #因为ovr数组的长度比order数组少一个,所以这里要将所有下标后移一位

    return keep

C

D. Bounding box regression


如上图所示，绿色框为实际标准的卡宴车辆框，即Ground Truth；黄色框为selective search算法得出的建议框，即Region Proposal。即使黄色框中物体被分类器识别为卡宴车辆，但是由于绿色框和黄色框IoU值并不大，所以最后的目标检测精度并不高。采用回归器是为了对建议框进行校正，使得校正后的Region Proposal与selective search更接近， 以提高最终的检测精度。论文中采用bounding-box回归使mAP提高了3~4%。


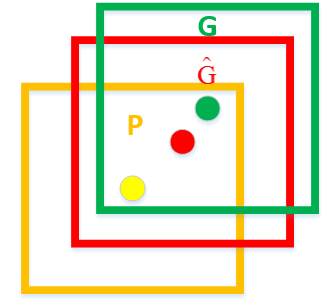
如上图，黄色窗口P表示Region Proposal，绿色窗口G表示Ground Truth，红色窗口表示Region Proposal进行回归后的预测窗口，现在的目标是找到P到红色窗口的线性变换（当Region Proposal与Ground Truth的IoU>0.6时可以认为是线性变换），使得红窗与G越相近，这就相当于一个简单的可以用最小二乘法解决的线性回归问题。

定义P窗口的数学表达式：
$$
P=\left ( P_{x}, P_{y}, P_{w}, P_{h}\right )
$$
分别表示P窗口的横坐标、纵坐标、宽和高，另两个窗口同理。

则P窗口的回归过程如下：
$$
\widehat{G}{x}=P{w}d_{x}\left (P\right)+P_{x}
$$
$$
\widehat{G}{y}=P{h}d_{y}\left (P\right)+P_{y}
$$
$$
\widehat{G}{w}=P{w}\exp \left ( d_{w}\left ( P \right ) \right )
$$
$$
\widehat{G}{h}=P{h}\exp \left ( d_{h}\left ( P \right ) \right )
$$

每一个d(P)都是一个Alex Net Pool5层特征的线性函数，即

$$
d_{}(P)=w_{}^{T}\phi _{5}(P)
$$

这里的